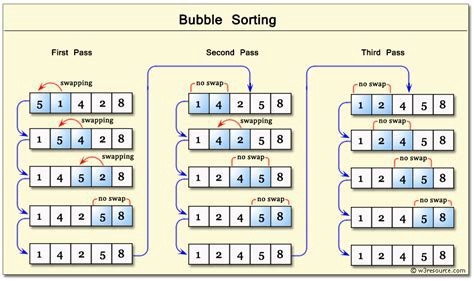
In my next few articles I want to talk about sorting algorithms, and how they work. When working with datasets you’ll want to organize them in all sorts of ways. Here I’ll talk about bubble sorts, and their basic construction.
It’s a fairly simple concept. Bubble sort will iterate through an array, and compare pairs. If the left index is bigger then the right index the values will switch. The algorithm will then move down one index, and compare again the two values.
The complication with this is that at each iteration the algorithm is just pushing the largest value to the end of the index since it is only looking at two indices at a time. So multiple iteration of the array is necessary. Our initial array [5, 2, 9, 1, 5] will look like [2, 5, 1, 5, 9] after the first pass.
So let’s code a bubble sort so we can get a better understanding of the nuts, and bolts.
The first part of our algorithm is the swap function. It’s a bit tricky because we’ll need to implement a temp variable to temporarily hold onto the index_1 position, otherwise it’s lost by the time I reassign it to index_2. Our swap function will take in array, index_1 and index_2 as parameters.

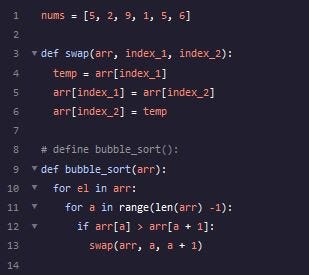
Okay, now comes the bubble_sort function. It begins by iterating through every element in the array. I’ll then loop again by the length of the array so I have the index of the element in case I want to swap.
Now if the index at that array arr[a] is greater than the one that comes next arr[a + 1] I’ll implement the swap function with the array, and current two indices.
Now, like any good programmer we should be asking: is there anyway I can make this more efficient?
We know that from the start the bubble sort is at least pushing the largest value to the end of the array, so each time we iterate over our array we really don’t need to check the last array again. We know that one is good. With that logic alone we can cut down the number of times we loop over our array by half!
So in our second loop lets minus our array by one for every loop like this:

for a in range(len(arr) - a - 1):

And there you have it! I wanted to share bubble sort as it’s a good introductory algorithm which opens the door to learning more complex algorithms. It answers the question, “How can we algorithmically sort a list?” and encourages us to ask, “How can we improve this sorting algorithm?”
Until next time — happy coding 🙂