You ever just study something that’s made you mad? Like programming doesn’t need to be this hard, and yet you still find yourself trying to understand Radix Sort. I’d like to promise you that everything is going to be okay, but you know what, we can’t know everything, and maybe some things are just worth sitting out.
Go home. I won’t be mad.
Now for the rest of you sadist sticking around I’m going to explain Radix Sort. Am I going to explain it well? I dunno yet, but explaining things helps me learn so if you don’t find this of service let me thank you for reading this. Because at this point it’s about me, so I thank you, truly.
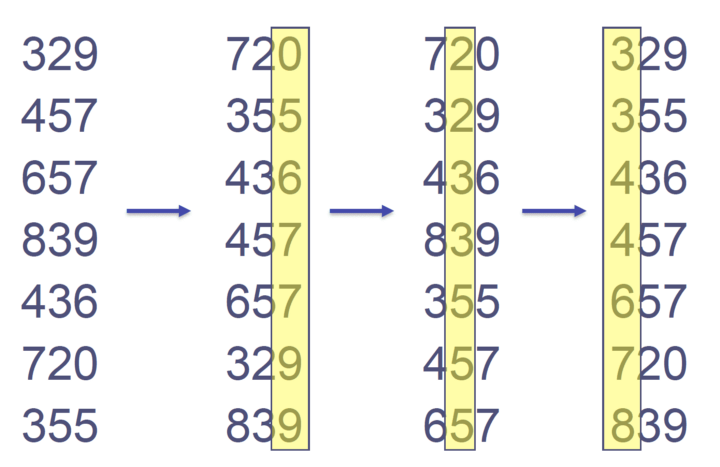
Let’s break this concept up. Radix is a sorting algorithm that looks at the whole number at each index, starting with the right most number. For example the number 824. First we look at 4, then 2, and last 8. We move our value around three times in accordance to 4, 2, and 8.
What do we move them around too? Well a list of ten list [ [], [], []…] we call a buck. Why ten? Because our Arabic numerical system has ten digits before it starts to repeat itself, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
So for our 824 number I’d move it into the 7th index (count from zero) on my first look. The next iteration I’ll move it into the 1st bucket, and the third iteration to the 3rd bucket.
It’s a weird, and beautiful way that this works when operated on a whole list of numbers. I don’t want to say magical, because it makes sense, but it’s some beautiful mind thinking.

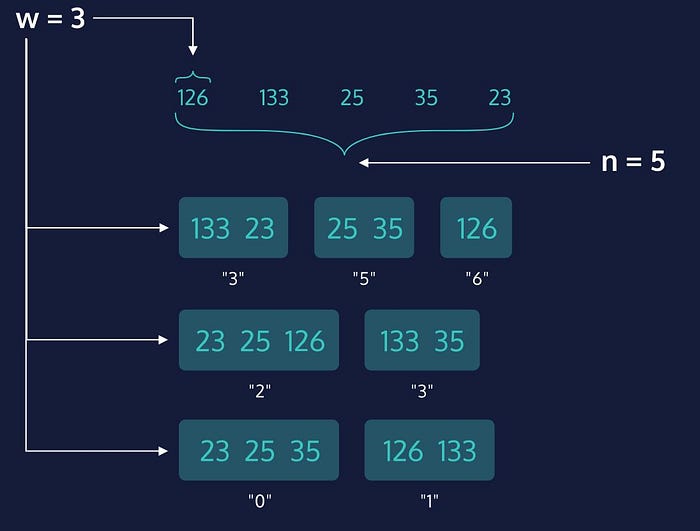
Above you can see Radix in action. It has a 3, 5, and 6 bucket on the first level. The second level has a 2, and 3 bucket, and the third level a 0, and 1 bucket. Radix will then flatten all the buckets into one list, and return a sorted list of numbers.
You may be wondering where the 0 bucket came from. Well Radix will look at the largest number in a list (above it would be 133), and see that it has three numbers. Radix will iterate 3x based on that, however 25, 35, and 23 only have two numbers. In this situation Radix will add a 0 in front of 25, 35, and 23 so it can keep the algorithm shuffling without missing a beat.
That’s Radix in a nut shell. Huh, maybe it’s not so bad after all.
The code is a bit different, because as you can see there are a few things to keep track of in order to properly conduct a Radix algorithm. Let’s list them out.
How many times Radix iterates is based on the largest number, and how many indices it has.
There are ten fresh buckets at each level of iteration to add our numbers to.
After the last iteration we flatten the bucket list into one array, and return it to the user.
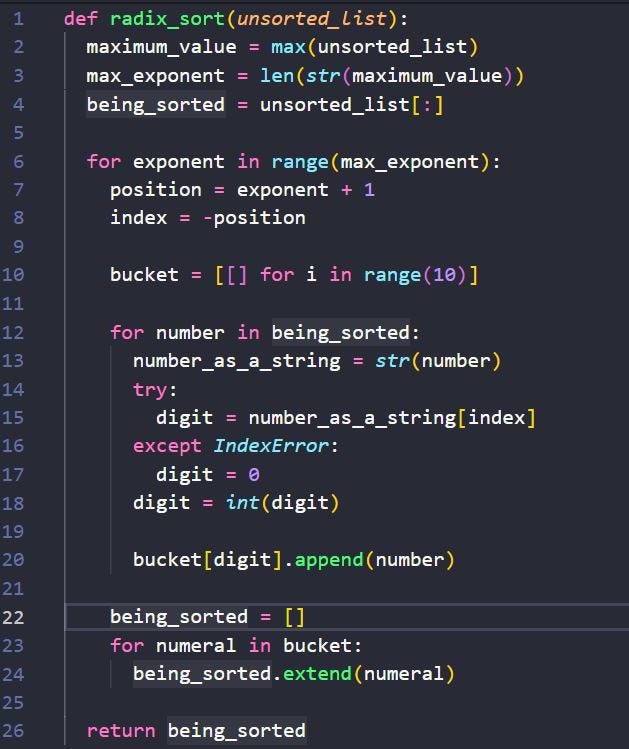
Let’s code! First let’s set up what we need to know in order to make this Radix hum smoothly. I’ll want to know what is the biggest number in the list, and it’s length. Is it a 3 digit number or 4? Maybe more. Also since we are iterating the list multiple times I’ll make a copy of the original list for safe keeping. It should look like:

def radix_sort(unsorted_list):
 maximum_value = max(unsorted_list)
 max_exponent = len(str(maximum_value))
 being_sorted = unsorted_list[:]

I had to change the maximum_value into a string so I could actually count it’s length. So that’s my basic need-to-know. Let’s start iterating based on that.

for exponent in range(max_exponent):
 position = exponent + 1
 index = -position

My index will be the last number in the exponent since that’s how python counts. We want to start from the number 4 in 824 so it will have to be list[-1] to grab ‘4’.
Now let’s set up our bucket array. Remember it’s just a list of ten empty list.

bucket = [[] for i in range(10)]

So we’re currently iterating on the length of the biggest number, let’s actually iterate over the numbers themselves.
I’ll embed a for loop over the being_sorted copy list created earlier. Each number needs to be turned into a string, and the string needs to be updated to be the last number in the list or our index (-position).
That way we can add it at the correct index of our bucket: bucket[digit].append(number).
But what happens when we reach a number that has only two indices like 24, when we are looping over 3 times because our biggest number was 452? Well I’ll use a try/except method, and make digit 0 so it can go/keep in front of the list. Here’s how that’ll look:

for number in being_sorted:
 number_as_a_string = str(number)
 try:
  digit = number_as_a_string[index]
 except IndexError: 
  digit = 0
 digit = int(digit)bucket[digit].append(number)

Now the last part is to flatten the list. After our above loop finishes our bucket will be ordered but still with ten lists inside of it. I’ll loop over the bucket and use the extend function to put everything back into the being_sorted array, and return it.

being_sorted = []
for numeral in bucket:
 being_sorted.extend(numeral)

My final Radix in all it’s glory:

I hope you still have questions, because I do too. Here’s a helpful video I found on youTube. Thankfully Radix sort has been figured out before us, so we can use it regardless how well we understand the underlining code. I do hope you understand the concept however. It’s also important to note that Radix is so well liked because it has a Big O of O(n) which is very fast.