Quick-sort is another divide and conquer algorithm like the merge_sort algorithm. Quick-sort’s unique method however makes it oddly efficient, and thus popular.
It’s a recursion operation, and calls upon itself to break an array into multiple sub-list. The final sub-list will have just one element left before it breaks out of its recursion with an assorted list.
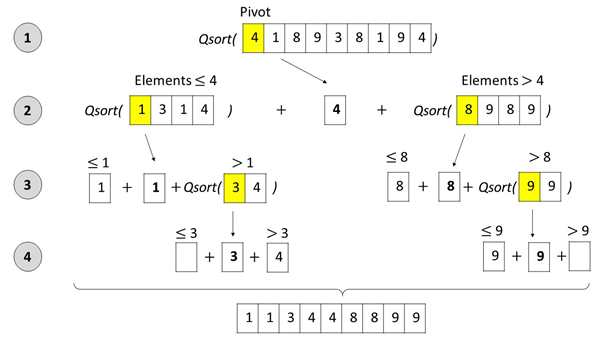
The idea is that on each level of the sub-list to grab a random element, otherwise known as the pivot, and compare it to the rest of the list, pushing smaller values to the left, and greater values to the right. Doing this will incidentally position our pivot element at the correct index of our list! Above you can see it first done with the number ‘4’. The operation is then repeated to the sub-list to the left with ‘1’ as its pivot, and ‘3’ as the last pivot.
Once it reached the last element all the values are ordered, so it just reconstructs itself, and presto! The left side of pivot ‘4’ is in order.
The same process is repeated on the right-side. Take some time to think it over. It’s a really clever algorithm. Let it marinate in the ‘ole noggin some to grasp it.
Quick note: quick-sort is rather efficient using the random pivot selector, because of the way it’ll divide a list, and split into a left and right side. The random pivot selection ensures you can’t really rig it to run it’s worse case scenario (which I won’t explain today). Quick-sort is that rare algorithm where we don’t describe it’s Big O scenario by it’s worse case situation, but rather its better case O(N * log N). It’s slip-through-the-cracks good. That’s all.
Alright, let’s get to the source code. Just like any recursion we need to establish the base case so we know when to pull the rip-cord, and exit our loop. We want to stop when our sub-list is just one element long.

def quicksort(list, start, end):
 if start >= end:
 return list

As you can see our parameters are the array itself, the start index (typically 0), and the end index being the length of the array minus 1 (because computers count from 0).
Next let’s build the logic for selecting a random index in the list. Thankfully python has a random module I can import to take care of that logic for me (randrange). Here’s how it’ll look:

pivot_idx = randrange(start, end)
pivot_element = list[pivot_idx]

So while I’m sorting things to the left or right of the pivot index where should I store that pivot index?
We’ll place it at the end of the array. That way it’s out of the way as I sort the rest of the array on that sub-list level. Once I’m done sorting I can bring it back to it’s place much easier. It works… trust me. If I’ve lost you check out my man KC Ang, and his explanation. Do note he conveniently has its pivot at the end of the array from the start.
So let me swap the random index with the last index:

list[end], list[pivot_idx] = list[pivot_idx], list[end]

Now we need our pointers. These are the objects that are going to keep track of our logic to sort our left and right sub-list (also called a partition).
The first pointer is our lesser than pointer that swaps indices with values less than our pivot index. The next pointer is our progress pointer that iterates down our list. Once our progress pointer finds a value smaller than the pivot it’ll call on the lesser than pointer to come switch spots to the front of the list.

Once we do a swap we’ll increase the index position of the lesser than pointer by one so it doesn’t just swap the same index every time.
Here’s how that’ll look:

See how the lesser_than_pointer starts at the beginning (start), and the for loop iterates the array. Once it finds an index less than list[end] it’ll perform a swap, and increased lesser_than_pointer’s index position by 1.
Once it’s done -outside the for loop we’ll want to move the pivot from the end of the array to the current position of lesser_than_pointer index where it belongs.

list[end], list[lesser_than_pointer] = list[lesser_than_pointer], list[end]

So that’s the whole operation at one level of the sub-list. To ensure that I will eventually meet the base case I’ll want to increase the start index by 1 so that the recursion will come to an end at some point.
That’s the whole operation for one level of the sub-list. In order to make it recursive I’ll simply call the function within the function, and away it’ll go!

Conclusion

I hope I broke it down well enough. Again this is tricky, and YouTube is always your friend. After some practice you’ll get it. The nice thing about recursion is that you just set up the first step. The rest is done on the stack repeating the function, so as long as you can build the first level your good, just don’t forget the base case so you don’t enter an infinite loop.