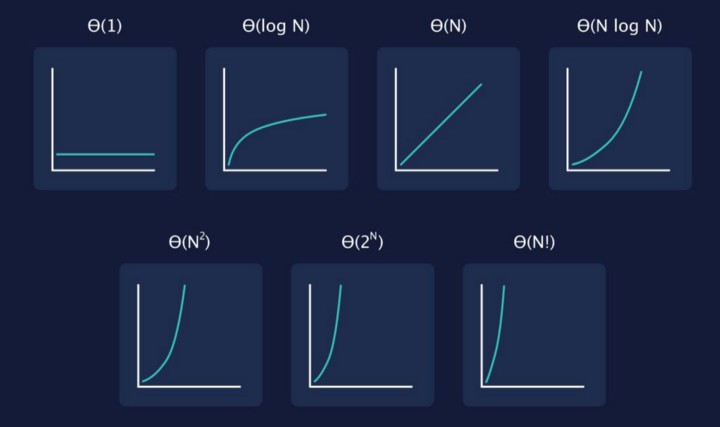
Coding is a powerful tool that can accomplish some real complex computations. It’s important that we write efficient code, even more so when dealing with large swaths of data, as that can take some real processing power, and not all computers are built equally. So when we talk about how fast a program is it’s not about hardware (although that helps), but in the code itself. How do we measure that? By using asymptotic notation. Don’t mind the alien space language it’s written in, because it’s not as bad as they want you think it is. Let’s demystify it together.
Asymptotic notation or A.N. measures in a general way speed of a code, by looking at the number of inputs taken. Inputs produce calculations. The more calculations your code needs to perform the more time it will take. Let’s look at an A.N. example:
5N² + 2N + 4
N is our number of inputs. When working with A.N. formulas we leave out the constants so our formula looks like:
N² + N
Why? Well asymptotic notations means ‘as n approaches infinity’. So that’s as big as a number as you’ll ever get. The constants are pittance in comparison, and thus don’t really matter.
Big Theta Θ is used when a code has one case to perform. Say iterating over a whole list array and printing it out. Well it would depend on how big that list is (which is our N) so we say the program has a run time of N or Θ(N). It’s a lot like one-for-one.
But say there’s some sort of logic to the function instead of just printing out ever item in a list. This logic could reduce the number of iterations our code will have to do. For example:

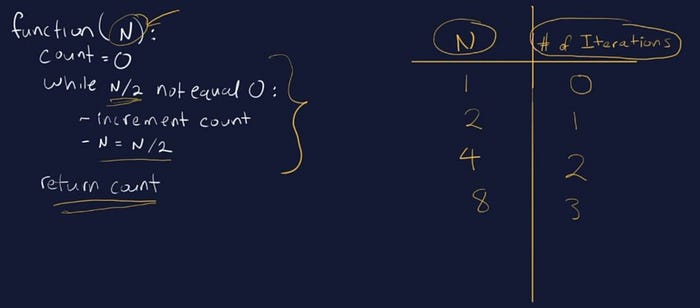
Here our while loop will increase the count while N/2 is not equal to zero. So if N is equal to 8 it’ll only iterate 3 times. The logic applied to it makes it more efficient based on the logic, and thus has a run time known as Θ(log N).

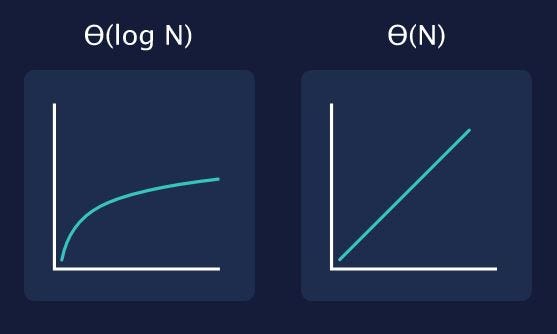
See how Θ(N) is steady and climbs evenly, because it loops through each iteration equally, while Θ(log N) starts off fast but begins to become more efficient as the logic of it’s code cuts down on the amount of work it has to do.
Now sometimes our code is really fast, or really slow based on luck. If our user had us iterate through a list looking for something, and it happened to be the first object in the list than our code was really fast. It could be the last object in the list, and our code had to go through the whole damn thing. The former being the best case scenario, or in alien language called Big Omega Ω. The latter or worst case scenario is known as Big O.
When analyzing our runtime we are typically more concerned with the Big O scenario. While it’s nice to get lucky, and land an Omega Ω situation it’s always better to prepare for the worst case. Even if you have a function that performs two different loops within it — the first loop running at Θ(N) and the second loop at Θ(log N), you would take the worse case loop and say the runtime big O is Θ(N).
What does an O(N²) look like?

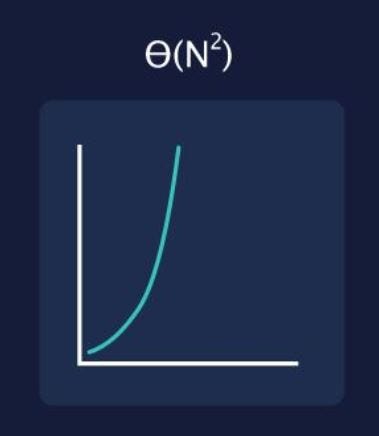
A good example would be a sorting list that has to iterate through a list, and place them in order. The loop will have to go through the list, and perform an additional computation upon it.
There are others A.N. to consider, but they just get worse. These basics are the most important to know. Getting a good understanding of A.N. will help you when you’re coding, and is something I keep in the back of my mind as I program.
Hopefully this helped demystify A.N. some. I know when the jargon and concept was first introduced to me it seemed as if it would be more complicated but the principles are simple.