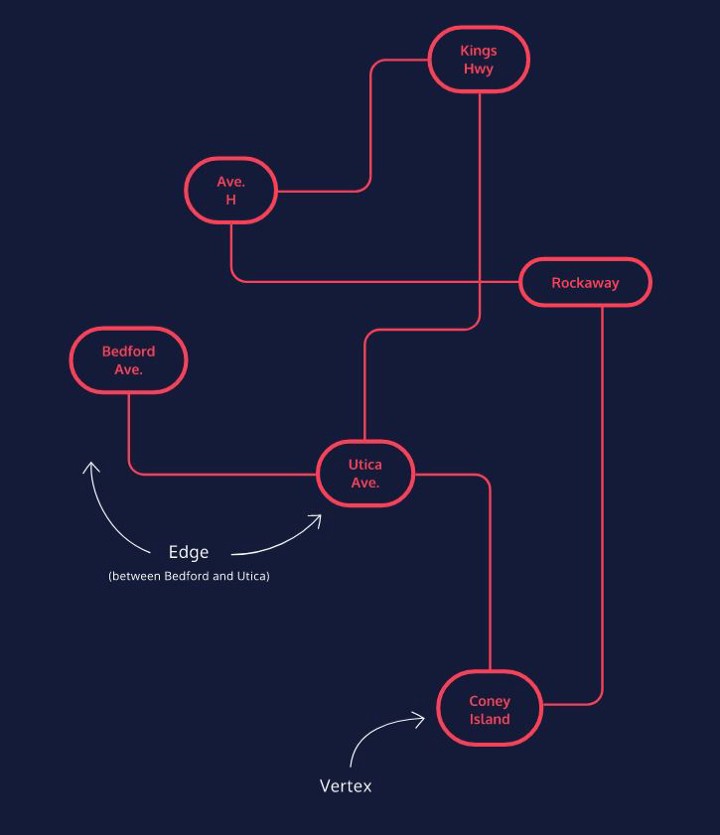
I wanted to talk about Python graphs as they are an essential tool in data structures. Graphs are a way to visual connections in a network. Above you can see vertices, which are the same as nodes that holds information. The links that connect them are called edges (no idea why, seems kinda silly to me). You’ll see these real world relations a lot in the professional world, so they’re essential to master. In this first article I’ll describe them best I can, so by the end we can move on to actually coding our own graph.
Graphs have varying degrees of connections. The more vertices a graph has the more links are abound as well. Edges between two vertices are bi-directional. Meaning you can travel in both directions.

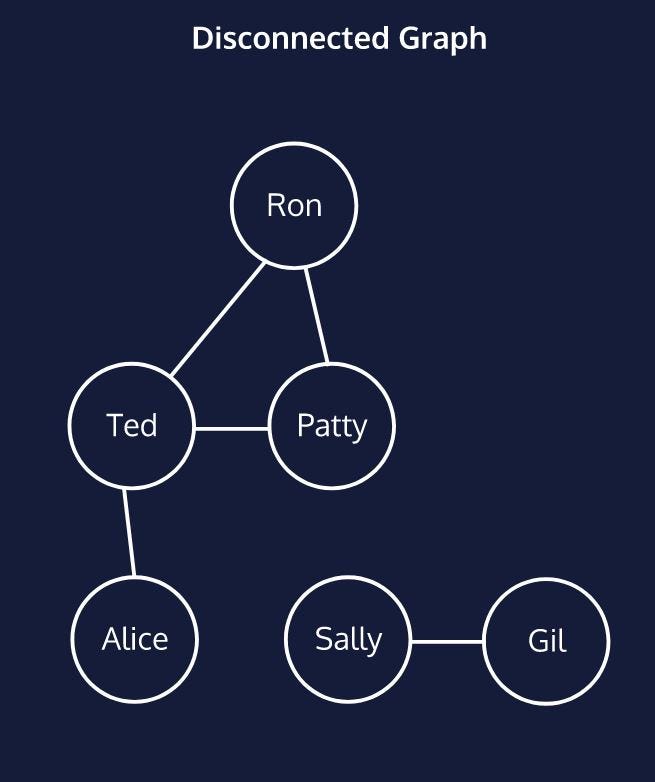
When two vertices are directly connected to each other such as Ron and Patty they are adjacent to each other. However Alice and Ron are connected by a path since they must travel through intermediaries to reach one another. Do notice that Sally and Gil don’t have any edges that could give them a path to Ron. This is know as a disconnect graph.
Another graph we have is a weighted graph where there is a cost to traveling the edges.

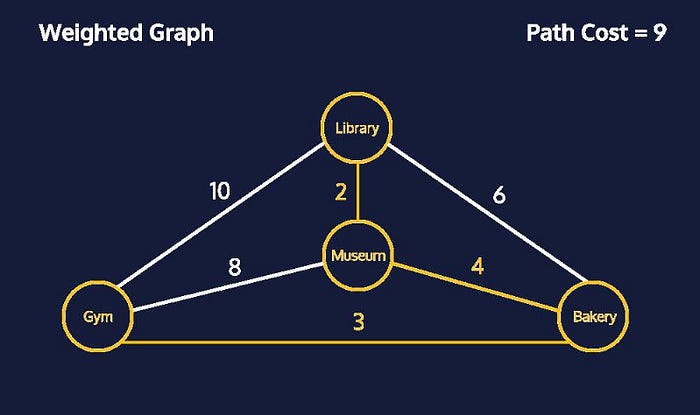
Not all paths are equal, and just because an edge is a direct connection to vertices doesn’t make it less costly. Above you can see it’s less costly to connect to the Museum vertex through an intermediary (Bakery) than to connect directly. The shortest path isn’t always the least expensive.

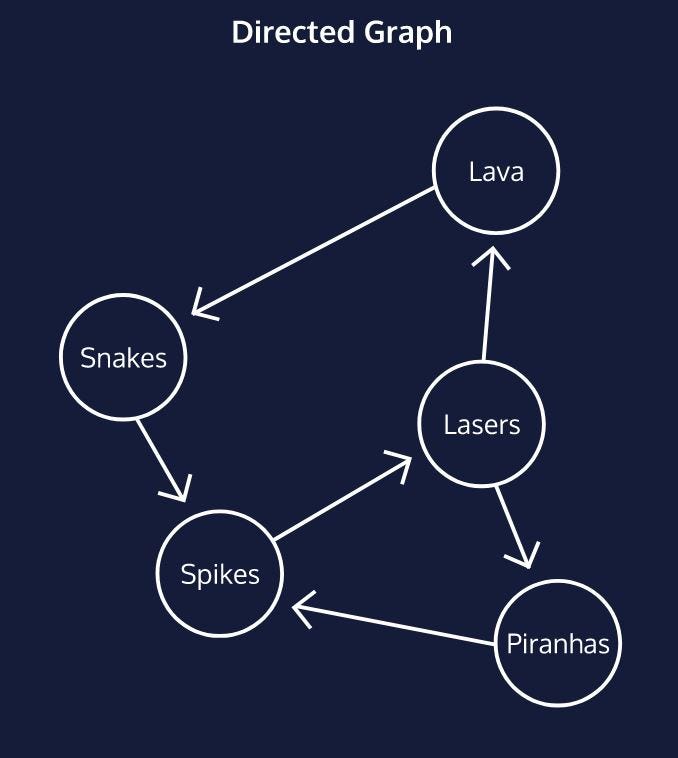
Directed graphs are graphs that do not have bidirectional edges, but edges that flow one way. Above you can see that it’s only possible to reach the “Snakes” vertex coming from the “Lava” vertex, but I could not go back to the “Lava” vertex from “Snakes”.
Pick any vertex to start from, follow it’s path and you’ll notice that it’ll lead right back to the vertex you started at. This is known as a cycle.

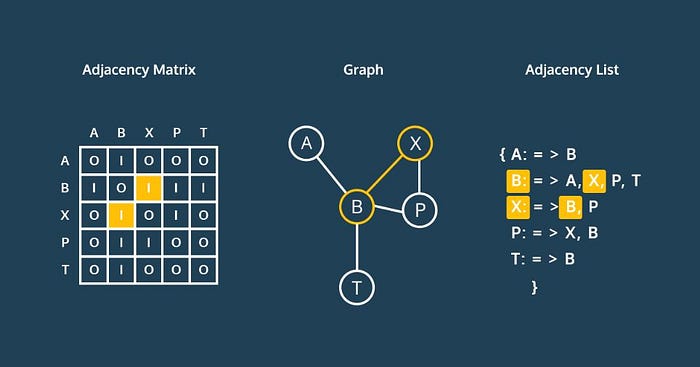
So how do we typically represent these graphs in a code friendly way? By using Adjacency Matrices, or Adjacency Lists. In a matrix the columns represent the vertices, as well as the rows since edges are bidirectional. A “1” represents a connection. An adjacency list simply is a dictionary that maps out connections. Take a look above, and you can see how vertex B and X are connected. Also note which aren’t connected.
How was that? Painless right? In the next article we’ll take a look at the code, and how these are set up.