As a programmer for about a year now most programming days are smooth sailing in comparison to the early days. I’ve learned how to learn, and with unlimited online resources I eventually stumble onto some actual materials of substance. I hope to add my own value to the vast knowledge so many others have graciously laid before me on the vast tubes of the internet. Hence this article on heap structures. It’s going to be heaps of fun, or so I hope because it one of the more difficult concepts to grasp the first time around.
So conceptually what are heaps? Heaps are basically a way to maintain a priority queue. Say we have a project that requires certain things be done in a certain order. Heaps will keep track of your progress, and maintain that order. Even if you happen to have done something out of order. It will readjust your heap structure/queue so that the order is maintained.
Heaps that track the minimum value, or max value are known as min-heap or max-heap. I’ll strictly refer to min-heaps, but as you can imagine the practice of maintaining a max-heap is fairly identical.
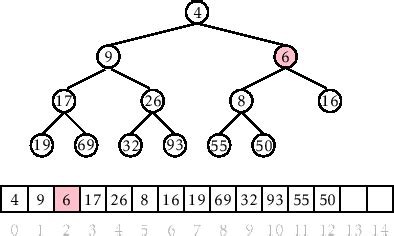
In the diagram above you can see that in a min-heap structure the parent nodes are of a smaller value then the children nodes. It’s clearer to see the structure as a binary tree. Beneath it you can study how it’s structured in an array. It can be a bit much to keep track of visually, so when we set up the the code we’ll implement helper functions to do the thinking for us. To grab the child node to the left we’ll use the index number of the parent, multiple it by 2, plus 1:
(index * 2) + 1
To grab the right node simple add 2 instead of 1.
(index * 2) + 2
To find the parent node use the following formula from the left child-node index:
(index -1) / 2
It’s important to grasp the concept so do take a look.
Next lets talk about adding a node to the structure otherwise known as heapify or heapifying. The over all concept is to add a node at the end of our array. We’ll then add code to check if the node is of a lesser value then it’s parent node. If it’s not then it’ll switch places with it’s parent node, and again check to see if it is less than its new parent. It will travel up our array until it meets our requirements, or ends up as the root node.
Alright what about removing a node? With a min-heap you’re probably working on a project to remove the smallest node first, so if we do grab from the root node, how do we maintain our heap structure? We’ll switch spots with our bottom node, and then pop off the last node in the array. Just like we would heap-up (heapify) when adding a node, this time we’ll heapify down till our structure is back in order.
Enough with the explaining, let’s code! Just like any python class we’ll define our most basic properties first. All we’re doing is keeping track of an array list, and a counter to help us later on when iterating through our array to make changes.

Our class is fairly useless at the moment. Let’s begin by adding a method to add to our empty heap_list (do note there is a None object inside it at index 0). To make this user friendly I’ll also add some print statements to help the end-user keep track of what is happening.

Our add method takes in the element to add, appends it to our heap_list, and adds 1 to the counter.
So adding an element is well-and-all, but let’s not forget if we have a full list already we’ll want to maintain the integrity of our array. Before I implement our heap_up method let’s add our helper formulas that’ll find: the parent, left child, and right child index.

Remember when we add an element to our list, we’ll start at the bottom, and compare the child node to the parent node, and heap upwards until the parent-child node rules are met (parent node > child node).

Let’s focus on our heap_up method. We’ll grab the index of our new node which is conveniently stored in the self.count constructor. I’ll then use a while loop to climb up from the bottom of the array to index one (remember None is at zero) traversing the parent indices using the helper function.
idx = self.count
while self.parent_idx(idx) > 0:
Within the loop let me designate what the child and parent index will be dynamically because as we are in the while loop they will change with each climb up.
The child will simply be the index set from the bottom and change as the while loop is performed: child = self.heap_list[idx], and the parent we can find with the helper function: parent = self.heap_list[self.parent_idx(idx)].
From here we can check the value of parent and child, and run a conditional if statement to make sure the parent is less then the child’s value. If not then switch.
if parent > child:
self.heap_list[idx] = parent
self.heap_list[self.parent_idx(idx)] = child

Now let’s change our idx from self.count to the parent index outside of the if statement. This will start the process all over again, so our while loop will check the new pair of parent/child nodes until it meets our heap requirements.
Make sure to put this method within the add() method so it’s done automatically, and doesn’t need to be specially called upon. We’ll always want our heap class to be in order.

Now let’s move on to removing a min node. Remember when setting up our heap_list we started with a None object. The min node will be held at position 1, not 0. So how do we remove the min node, and keep our array structure in tact? Well we’ve got a clever method where we just switch the first and last node, and pop() off the min node to retrieve it.

I’ll add some helpful print functions, and minus the self.count. It’ll look like this:

Okay, I know what you’re thinking. Our array is out of sorts, and just like we heaped up before this time we’re gonna head down our array.
So heaping down is a little different compared to when we went up. Going up we only had to compare the new node with the parent node. Going down we have two nodes (left and right) to choose from. To keep our heap structure we’ll want to swap with the smaller node. Let me show you an example:

After swapping 21 and popping it off should 42 go to the left or the right? Hint: it’s to the left (36).
We’ll need a helper function called get_smaller_child_idx(). First let’s find if a right index exist -sometimes it don’t. If there isn’t just return with the left one otherwise create a left and right variable with the values of the nodes at their respective index. Then using an IF statement find out which child is smaller. The left or right.

Okay, let’s move to the heap down part. We’ll need a while loop that will function as long as we have children elements to compare against. So we’ll set our index at 1 to begin. We’ll then get the smaller_child_idx() of index 1. We’ll compare if the parent is greater than the child. If it is we’ll swap the index/parent as the child, and the smaller child up as the parent. We’ll then reset the index to the moved down child, and check again if it meets the qualifications to heap down again.

I’ll then add this function to the retrieve_min method so it’ll automatically be done whenever I retrieve the min node.
And it’s done! That’s your basic heapMin Class structure. It can be a bit much with the juggling of nodes, but it’s all there. I know I found it a doozy the first time.
I hope this made it a little easier.