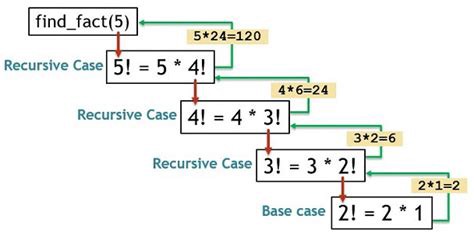
Recursion are an interesting, and tricky concept in our Python tool box. Basically it’s when code goes meta, and calls upon itself to execute a self function until it meets a base requirement to exit the loop. These sorts of algorithms are used for iterating over a list.
So why use recursion when we already know loops? Recursion is simpler than an iterative-loop solution, usually because it exploits a structural aspect of the problem in a way that the iterative-loop approach cannot.
Loops will loop over controlled variables, using your typically conditional statements (if, for, while, do while) and are memory efficient while recursions loop over themselves using if/else statements with a base case to break out of it. Recursion are also a memory hog. Everything done by a loop can be done by a recursion, but not everything done by a recursion can be done by a loop. Recursions are great for traveling through a binary tree graph making them important to understand.
So how do recursions work. Like literally? Well like I said recursions call upon itself, and has a base case to break out of it self. For example:

def sum_to_one(n): if n == 1: return n print("Recursing with input: {0}".format(n)) return n + sum_to_one(n - 1)

Above our base case is if n == 1 return n, our recursion below it is return n + sum_to_one(n-1).
Say n equals 7 it will see that it doesn’t equal 1 so it’ll return 7 plus the function again however n is minus 1 taking me to 6.
So the next go-around the inside function will see that n equal to 6. It’ll return 6 plus the function again however n is minus 1 again, and repeat the function using n as 5. This process repeats until it reaches the base case and starts to return n from each inner function … 1, 2, 3, 4, 5, 6, 7. We then add that to what n is at the moment as the formula stipulates, and it looks like:

1, + 2, + 3, + 4, + 5, + 6, + 7 = 28.

This is a great way to start from the top of a list, and perform an operation at every level, till your reach a base case and climb out.
There is however something out of view in this operation that our Python code performs that you don’t see, and that is the stack. While our recursion is climbing down our array the program is keeping track with each step so it can climb out. It’s doing this by stacking the code in it’s memory.
>Let me show you an example using a while loop:

def sum_to_one(n):
 result = 1
 call_stack = [] while n != 1:
  execution_context = {"n_value": n}
  call_stack.append(execution_context)
  n -= 1
  print(call_stack)  print("BASE CASE REACHED") while call_stack != []:
  return_value = call_stack.pop()
  print("...adding {0} to result {1}".format(return_value["n_value"],   result))  result += return_value["n_value"]
  print(call_stack) return result, call_stack

Above I set up an empty call_stack variable to be filled in. And a while loop to iterate over n as long as it doesn’t equal 1. I’ll then add the current n value to the call_stack, and decrement n by 1 at each loop so I eventually reach the end. Our call stack is now filled.
In my next while loop I’ll call upon the call_stack, pop out the last value, and add it to my result variable, performing my choice of mathematical operation.
Using a recursion all this is self implied.
The stacks are important to be aware of, because if a stack is too big it can crash our program (known as a stack overflow) hogging all the memory we have, so use accordingly.
Let’s look at another recursion a little differently. I’ve imported a list of planets, however while importing it some of the planets were in a sub list of their own. So instead of a simple flat list I’ve got this:

planets = ['mercury', 'venus', ['earth'], 'mars', [['jupiter', 'saturn']], 'uranus', ['neptune', 'pluto']]

How can I use recursion to flatten my list? Well here I don’t need to perform a recursion on ever object in the list, just the list objects in my list. Here’s how I’d build it.

def flatten(my_list):
 result = [] for a in my_list:
  if isinstance(a, list):
   print("List found!") 
   flat_list = flatten(a) ## recursion!
   result += flat_list  else:
   result.append(a)
 return result

I used a for loop to iterate through my list, and if it catches a list within my list I’ll unleash a mighty recursion to repeat the process that is the original purpose of this function. All the while appending it to my result variable. Quite elegant, isn’t it?
Of course there’s a lot more you can do from here, but I’ll keep it simple for now. I just wanted to dip your toe into the general understanding of recursions, as it can be a difficult concept to grasp at first.