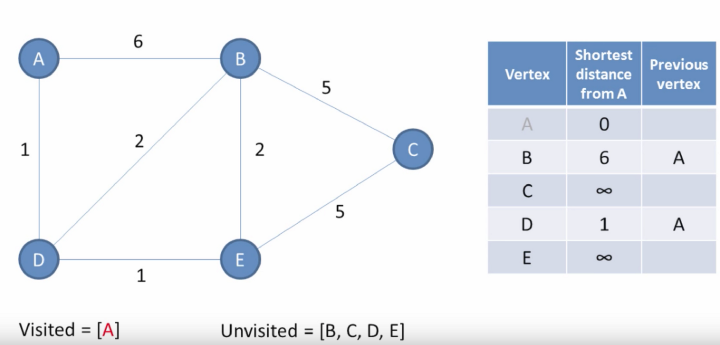
Dijkstra’s algorithm is an algorithm used to find all of the shortest distances between a start vertex and the rest of the vertices in a graph. Above you can see we start at A, and from there we will find the shortest distance to all other vertices. Dijkstra uses breadth-first search algorithm, and updates the cost of each edge updating the cost-list when it comes across an edge path that is less than what it already has.
From the start we assume every edge has a cost of infinity (this is impossible) so when it comes across the first edge cost of that link it will update it, because naturally it will be of a lesser value. Going forward as the algorithm moves among vertices it will keep updating with anything that is less as it searches the graph.
I recommend seeing it visualized as it can be difficult the first time you learn about it.
Let’s see how we can code Dijkstra, and it may make more sense. What we’ll need to begin is a dictionary of our weighted graph that shows it’s neighboring vertices, and their weight cost. I’ll also use some built in python libraries to help me pop and push our vertices from our heap (Dijkstra is optimized to be used with a heap graph). I’ll use a second library to set the infinity value as well to make life easier.

from heapq import heappop, heappush
from math import inf
graph = {
'A': [('B', 10), ('C', 3)],
'C': [('D', 2)],
'D': [('E', 10)],
'E': [],
'B': [('C', 3), ('D', 2)]
}

Okay now we’re ready to build the Dijkstra. The purpose of this function is to return use the shortest distances from our targeted vertex in the graph. We’ll use A in this example. So we’re building a distances dictionary, and in the end returning it.

def dijkstra(graph, start):
 distances = {}
 return distances

Now we’re ready to loop over the vertices in our graph. Remember every vertex starts at infinity so I’ll assigned that now, and after I’ll reassign our A vertex to zero, because it is our start vertex. I’ll also add a list with a tuple. This tuple represents the start vertex within the min-heap list. Well pop off the vertex in it as we search, and if there is a neighbor we’ll push it into the tuple list so it’ll keep searching. Once there’s no new neighbor it’ll be empty, and end our while loop.

def dijkstra(graph, start):
 distances = {}
 for vertex in graph:
  distances[vertex] = inf
 distances[start] = 0
 vertices_to_explore = [(0, start)]
 return distances

Let’s jump into the iteration with the while loop. Remember it’s runs based on the vertices_to_explore tuple. We’ll pop it off so we get the distance 0, and vertex (A) in individual variables.

while vertices_to_explore:
 current_distance, current_vertex = heappop(vertices_to_explore)

Now let’s loop over the graph at the start (A) vertex. I’ll want the neighbor’s of start (A), and their edge weight. I’ll calculate their edge weight with the addition of our current vertex. The first one being 0.

while vertices_to_explore:
 current_distance, current_vertex = heappop(vertices_to_explore)
  for neighbor, edge_weight in graph[current_vertex]:
   new_distance = current_distance + edge_weight

Now if this new weight is less than the current weight (and the first time it will always be less than infinity) then replace the two values.

while vertices_to_explore:
 current_distance, current_vertex = heappop(vertices_to_explore)
  for neighbor, edge_weight in graph[current_vertex]:
   new_distance = current_distance + edge_weight
    if new_distance < distances[neighbor]:
     distances[neighbor] = new_distance

And then to keep the while loop going we’ll push into vertices_to_explore the neighbor vertex of this current for loop.

while vertices_to_explore:
 current_distance, current_vertex = heappop(vertices_to_explore)
  for neighbor, edge_weight in graph[current_vertex]:
   new_distance = current_distance + edge_weight
    if new_distance < distances[neighbor]:
     distances[neighbor] = new_distance
      heappush(vertices_to_explore, (new_distance, neighbor)
return distances

Conclusion

That’s it. Not too crazy. Dijkstra’s algorithm is great for finding the shortest distance from a start vertex to all other vertices in the graph. However, it is not the best when we are just looking for the shortest distance from a single start vertex to a single end vertex. That’s where we’d need to take into another variable into consideration. The actual relative distance of two physical locations -like on a map. That algorithm is known as A* (a-star). It’s far too complex for me to write an article about, but if you found Dijkstra useful I’d highly recommend checking out A*!