I wanted to discuss two types of graph search algorithms, as they are important concepts in working with graph structures.
The first is known as Depth First Search (DFS). As you can see in the gif above it travels down the vertices of a graph one by one via its connected vertex. Once it reaches the end of the branch at vertex #4 it checks back with vertex #1 to see if there was another neighboring vertex to run through. DFS methods are great for graph structures that are built long like a string -without a lot of branches to explore.
The second search algorithm Breath First Search (BFS) works better on structures with a lot of branches. It will first look at all the connected vertices. So instead of going 1 -> 2 -> 3 -> 4 as DFS does above –BFS will go 1 -> 2, 1 -> 5, 1 -> 9. BFS looks at all the neighboring vertices connected to #1 before going deeper. It travels much more spread out like a breath… (I don’t name these things)
So what are the mechanics/logic that makes these algorithms work. Once we understand that we can move on to the actual coding. Lets look at DFS.

When performing DFS we’ll need two things: a visited array, so we know where we’ve been, and a stack to retrace our steps once we’ve reached the end of a branch, and need to climb out of it.
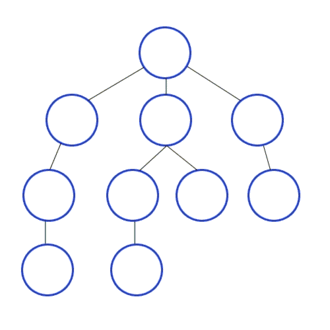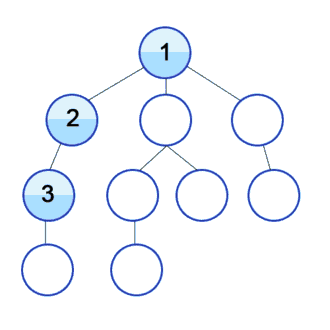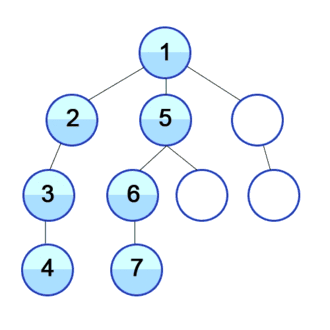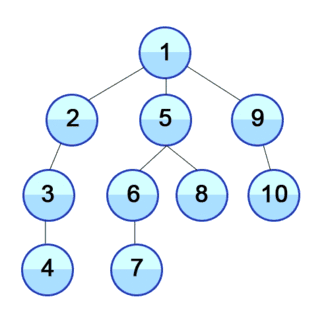
Above we travel 1 -> 2 -> 4 -> 9 -> 7. Once we’ve reached 7 there are no new vertices to visit, so at this point I’ve either traveled the whole graph or just got to the end of one branch in particular. How can I know which case it is? By using the stack. Once I can’t travel to a new vertex I’ll start popping off the vertex in my DFS stack one-by-one. Off goes 7, and at 9 I still don’t have a new vertex to visit. Off goes 4, but at vertex 2 I see I can travel to 8. From 8 I’m stuck again and go back to 2, then 1. This process repeats, and once my stack is empty I know I’ve traversed the whole graph.
Pretty cool. How about BFS?
BFS visits every connected vertex so to keep track of where to move next we’ll use a queue instead of a stack.

BFS starts at 1, and instead of only going to vertex #2 it goes to #3 as well. We add 1, 2, and 3 to the queue. Once we see that vertex #1 has visited all available vertices I’ll pop #1 off of the queue, and start from #2. #2 will then look around, and add to the queue #4, #7, and #8 -as they are connected to #2. I’ll repeat the process till all vertices are visited, and the BFS queue is empty.
The important distinction to make is that BFS exhaust every connection before moving forward in the queue, where as DFS moves forward every time it visits a new vertex.
Part II — The Code
Now that we understand the concepts of our DFS and BFS algorithms let’s take a look at how we would construct the code with DFS first.
Let’s consider what we would like to enter as parameters. We’d need the graph, the current vertex, and the target value. Remember that we’ll need a list to keep track of our visited vertices, and since this will use a recursive method we’ll want to pass that visited list into the function as a parameter too. However, the first time we call this function there’s no list to enter. We’ll give it a default value of None, and let it fill itself in during the recursion. Read that twice if you need to. That stuff trips me up the first go around.
def dfs(graph, current_vertex, target_value, visited=None):
Now we want our visited to be redefined if it’s not in a recursive call -the first invocation. It’ll start with the current_vertex since that’s where we begin. I’ll then return this new version of visited.
def dfs(graph, current_vertex, target_value, visited=None):
if visited = None:
visited = [current_vertex]
return visited
Now as always for a recursion we need a base case, and what I want is for the visited list to be return once the current_vertex is equal to the target_value.
if current_vertex == target_value:
return visited
Okay, from here let’s set up the recursion. What we want is to check the neighbor vertices of our current_vertex. To do that we’ll just use a for loop. If that neighbor vertex hasn’t been visited I’ll want to create a path variable. The path variable will be the function called again (recursion) with the new current_vertex being the neighbor vertex. If I made a new path it’s because I haven’t found the target_value yet, so I’ll want to return the path at each step so I know how the path was formed thus far in my search. I’ll return the path if there is one to return.
for neighbor in graph[current_vertex]:
if neighbor not in visited:
path = dfs(graph, neighbor, target_value, visited)
if path:
return path
Not to bad right? The hardest part is just thinking the steps through, but the code isn’t too far out there.

Let’s see how BFS compares. BFS is primarily concerned with the shortest path from current vertex to the target, and as it explores all paths in a while loop (no recursion) we can set the path, visited, and queue inside the function. Here’s how it’ll look.
def bfs(graph, start_vertex, target_value):
path = [start_vertex]
vertex_and_path = [start_vertex, path]
bfs_queue = [vertex_and_path]
visited = set()
Next is setting up the conditions of our while loop. We’ll want it to run as long as our queue is filled with vertices. We’ll want to pop off the vertex in the queue so it doesn’t run forever, and add it to the visited list so we known we’ve been there.
Inside the loop body, use Python’s multiple assignment to set the new variable current_vertex and path equal to the first element on bfs_queue.
while bfs_queue:
current_vertex, path = bfs_queue.pop(0)
visited.add(current_vertex)
That’s some fancy code juggling action.
So we got our queue pop’n, and our visited array accruing each new vertex. Let’s visit the neighbors of each vertex in a for loop. Now I want to check if the neighboring vertex isn’t in the visited list. If it’s not, and if it’s the target_value then BOOM I found my path. I’ll append that neighbor to the path array, and return the path.
for neighbor in graph[current_vertex]:
if neighbor not in visited:
if neighbor == target_value:
path.append(neighbor)
return path
Now if the target_value isn’t found I’ll want to add this neighbor to the queue, path plus neighbor. To handle the case that we need to keep searching because neighbor is not the target_value.
for neighbor in graph[current_vertex]:
if neighbor not in visited:
if neighbor == target_value:
path.append(neighbor)
return path
else:
bfs_queue([neighbor, path + [neighbor])
And that’s it. Here’s the final shape of our BFS (with DFS to compare) function.

I hope this helped clear up any confusion you had. Happy coding!